Dispersion of a Gaussian pulse
Dispersion of a Gaussian pulse
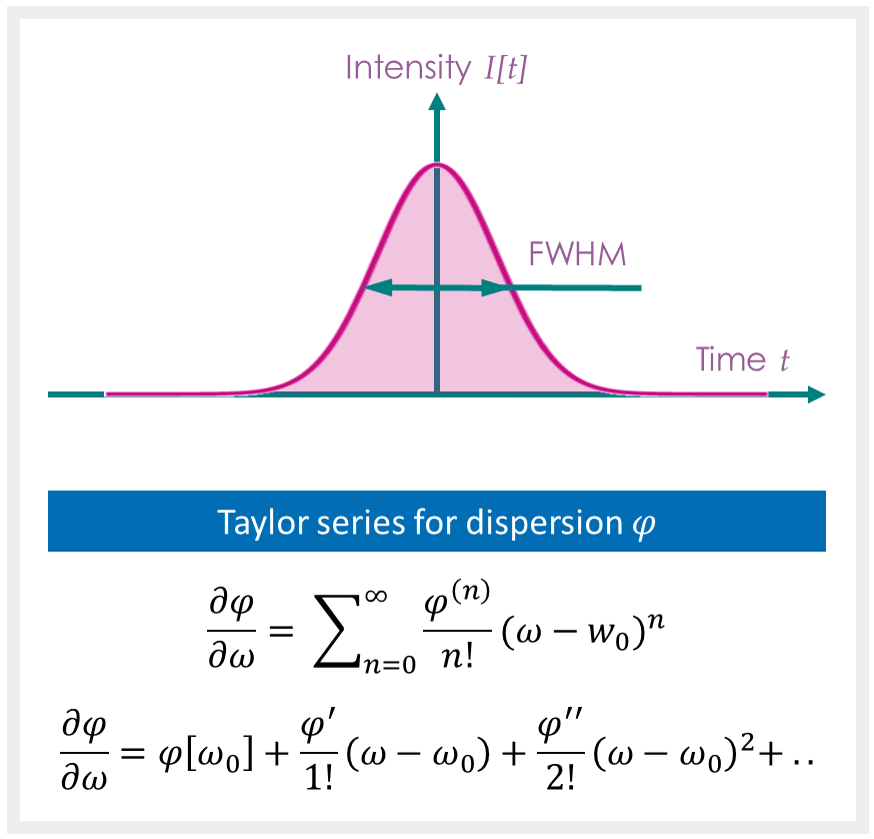
The temporal intensity profile \(I [t]\) of a Gaussian pulse can be represented by
$$ I[t] \;=\; I_0\;e^{-\frac{t^2}{\tau^2}}. \tiny{\tag{1}}$$
Herein, the pulse duration \(\tau\) is defined at the \(1/ e^2\) level, which represents 13.5% of the peak intensity. The pulse duration at full width half maximum (
FWHM) can be calculated by use of
$$\tau_{\scriptsize{FWHM}}\;=\; \tau_{1/e^2}\;\sqrt{2 \;ln[2]}. \tag{2}$$
The pulse duration of a Gaussian pulse changes due to group delay dispersion \(\phi^{''}\) (GDD). The dispersed pulse duration is
$$\tau^d_{\scriptsize{FWHM}} \;=\; \frac{\sqrt{\tau^4_{\scriptsize{FWHM}} + 16 \phi^{''2} ln[2]^2}}{\tau_{\scriptsize{FWHM}}}.\tag{3}$$
In eq. (3), the group delay dispersion GDD is defined as commonly done through the Taylor series describing the dispersion of the system around a center frequency \(\omega_0\).
When propagating through dispersive material, GDD is
$$GDD\;=\;GVM\;l \tag{4}$$
where \(GVM\) is the group velocity mismatch and \(l\) is the length of the material.